区間縮小法とはある区間をどんどん狭めていくと、ある一点に収束するよねって主張です。
直観的には当たり前だろって主張なんですけどね。自明のことですら厳密に証明していくのが数学ですからね。
この証明には単調増加数列の性質を利用します。
区間縮小法
部分集合
区間縮小法の話の前に数学というか論理記号の意味を補足します。
$A \subseteq B$
Uの字を横に倒して=をつけたような記号です。
これは「AはBの部分集合です」の意味です。
ただこれは広義の部分集合を示しており、A = Bの可能性があります。
AはBの部分集合ではあるんだけど、Aそのものである可能性は否定していません。
そこで、A ≠ Bを約束する狭義の部分集合として
$A \subset B$
が定義されています。
閑話休題。
それでは話を進めていきます。
まずはある集合$I_n = \{I_1,I_2,I_3,…\}$を定義します。
この$I_n$は単調減少で
$I_1 \subset I_2 \subset I_3 \subset…$
となります。
※nが増えるに従い集合の区間の幅が徐々に小さくなるとイメージしてください
また集合Iはどの範囲においても空集合でない必要があります。
$I_n = \varnothing$
※Iはびっしり詰まっているとイメージしてください
$\bigcup$は集合を表し、nを1から∞まで増やしてもその中にCが存在していることを示しています。
$\bigcup_{n = 1}^{\infty} I_n = \{C\}$
どのnをとっても(どれだけ幅を小さくしても)区間Iは空集合ではなく、ある値Cが必ず存在していることを証明できれば、一点に収束することが証明できます。
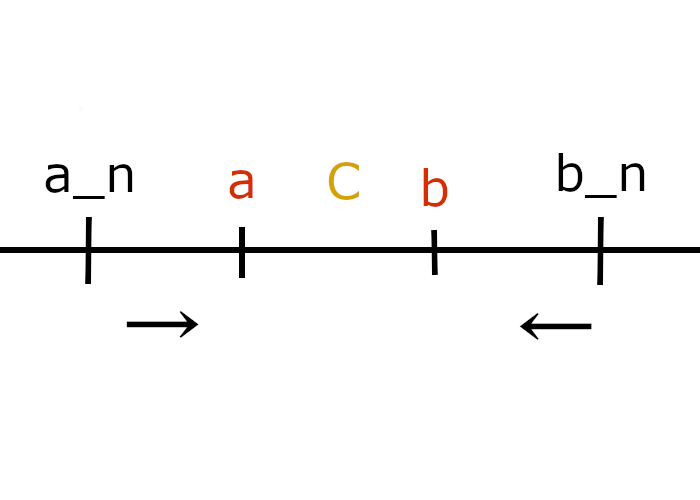
そのために単調増加数列の$a_n$と単調減少数列の$b_n$を定義します。
区間Iの範囲をこれらの数列を使って表します。
$I_n = [a_n,b_n]$
[]の意味は
$a_n \leq I_n \leq b_n$
です。
$a_n,b_n$は単調増加数列と単調減少数列なので、性質により極限をとるとある値に収束します。
$a_n$が収束する値をa、$b_n$が収束する値をbとすると区間Iはこうなっていることになります。
$a_n \leq a \leq C \leq b \leq b_n$
極限をとると$a_n$はaに$b_n$はbに収束していきます。
大小関係より$I = \varnothing$ではありません。
また、この区間の幅を限りなく小さくしてくってことは
$a_n – b_n = a – b = 0$
でもあるので
$a_n,b_n$の収束先のaとbが同値であり、また[a,b]区間Iにはぎっちり詰まっているので、どんなに区間を小さくしてもCは存在します。
つまり
a = b = c
同値であることが言えます。
nを無限に大きくすればCに収束するのは直観的に分かりますね。
直観的に自明のことではありますが、数学的な論理に当てはめるとこうやって説明するってことですね。
ここまでの流れを追うとこんな感じ。
実数の性質
上に有界な集合は上限を持つ
↓
単調増加数列の性質
単調増加数列は収束する
↓
区間縮小法の性質
数列の区間をどこまでも小さくしていけばある点に収束する
論理を解読する威力
直観的には自明なことをわざわざ論理的に証明しているのは、数学という学問が直感が働かなくなるような領域へ足を踏み入れているからです。
一見すると当たり前のことでも、その論理の構造がどうなっているのかを解き明かすことは大切なことです。
直観的には共通点が見いだせないような領域であっても論理的には一括りに扱えることがあります。
逆も然りです。
つまり一般化することで世界観が一変することがあるんです。
一見すると同じに見えるパンチの打法ですが、論理構造を解読することで2種類に分類することができました。
そうすると、これまで気がつかなかった二種類の打法の輪郭がくっきりと浮かび上がってきました。
抽象的な打法の概念をさらに一般化することで野球などの別のスポーツへ応用できることにも気がつきました。
またパンチの打法が別の自動システムという点に細い線で繋がっていることにも気がつくことができました。
自明のことであっても論理を解くことで一見すると無関係に見えたものが繋がっていきます。
数学が自明であることを手間暇かけて、執拗なまでに証明しようとする性格をしているのは、論理構造を解読することの威力を知っているからでしょうね。


コメント