数学って深すぎますね。
実数の性質について学んでいたはずが、気が付けばベクトル空間って底なし沼に足をとられています。
僕は搔い摘んで学んでいるのである程度の速度を保って前進できていますが、本当に理解しようとすれば途方もない時間と労力が必要なのを感じます。
それこそ廃人でもないと数学の深いところにはたどり着けません。
前回はベクトル空間を$\mathbb R^n$の実数の世界に広げていきました。
ベクトル空間の公理を満たせれば、それがどんな形に見えようとも、それはベクトル空間です。
今回は前回の続き。ベクトル空間の適用範囲を広げていきます。
数列
数列$a_n$はある角度で見れば縦ベクトルの座標を表す点が無限にあるだけだと言えてるので、加法とスカラー乗法をうまく定義できればベクトル空間の公理が満たせます。
$\left(\begin{array}{c}a_1\\a_2\\a_3\\ \vdots \\a_n\end{array}\right)$
こんな風に数列は縦ベクトルが無限に続いているとも見れます。
$n^2,\frac{1}{n}$みたいなものが数列です。数列は実数空間に含まれているので前回の話が理解できればそこまで難しくはないと思います。
数列の同じ項同士を足し合わせることを加法、各項を実数倍することをスカラー乗法と定義すればベクトル空間の公理を満たします。
面倒なので公理を満たすかどうかの証明は省きます。
加法の定義
$\left(\begin{array}{c}a_1\\a_2\\a_3\\ \vdots \\a_n\end{array}\right) + \left(\begin{array}{c}b_1\\b_2\\b_3\\ \vdots \\b_n\end{array}\right) = \left(\begin{array}{c}a_1 + b_1\\a_2 + b_2\\a_3 + b_3\\ \vdots \\a_n + b_n\end{array}\right)$
スカラー乗法の定義
$k\left(\begin{array}{c}a_1\\a_2\\a_3\\ \vdots \\a_n\end{array}\right) = \left(\begin{array}{c}ka_1\\ka_2\\a_3\\ \vdots \\ka_n\end{array}\right)$
写像
僕が少し難しいと感じた部分です。
何故かといえば「写像」という概念自体がピンとくるほど理解できていないからです。
「写像」の論理は分かりますが、日常的に使うことがないのでイメージ(画像とか動画)が頭にないような感じ。
正しいイメージが頭の中に形成されるといちいち理屈で考えなくても直観で答えが出てくる感じがありますけど、今はイメージがないから直観が働かないというか、思考が働かないというか。そんな感じです。
閑話休題。
写像がベクトル空間であることを見ていきます。
その前に「写像とは何か?」ですが、写像は関数を抽象化した概念です(多分)。
ある集合の要素とある集合の要素を結びつける規則を写像と呼びます。
$y = x^2$はxの集合とyの集合との関係を示しています。その時の規則が二乗です。
詳しくは以下のリンクを見てください。
写像がベクトル空間の公理を満たすための要点はその演算の定義の仕方。定義は人間が勝手に決めた、決められるものなのでどうやったていいものなんですが、テキトーに決めると実数の演算のようには振る舞ってくれません。
演算をどう定義すればベクトル空間として扱えるのか、昔の数学者は写像の演算をどう定義したのか見ていきます。
写像の加法
$f + g: x \to f(x) + g(x)$
f,gの写像を足して得られた新たな写像は、f(x)とg(x)の値を足したものと同じになるようにって定義されています。
左辺の+は写像の足し算、右辺の+は実数の足し算を表しています。
つまり、写像の足し算は実数の足し算に変換できると定義しています。
関数だともう少しわかりやすくて
$(f + g)(x) = f(x) + g(x)$
左辺は関数の足し算、右辺は普通の実数同士の足し算。
右辺はf(x)とg(x)を足して新たな関数(f + g)(x)を作ることを表していて、左辺はその関数がどのように振舞うべきかを示しています。
(f + g)(x)に1を入れた時の値はf(x)に1を g(x)に1を入れた値を足し合わせたときの値になるようにとの要請です。
写像の乗法
スカラー乗法はこう。
$af:x \to af(x)$
写像fをa倍した写像とは実数f(x)をa倍したもの。
関数だと
$(af)(x) = af(x)$
a倍の関数は、ある関数に実数を入れて返ってきた実数をa倍したものだと定義されています。
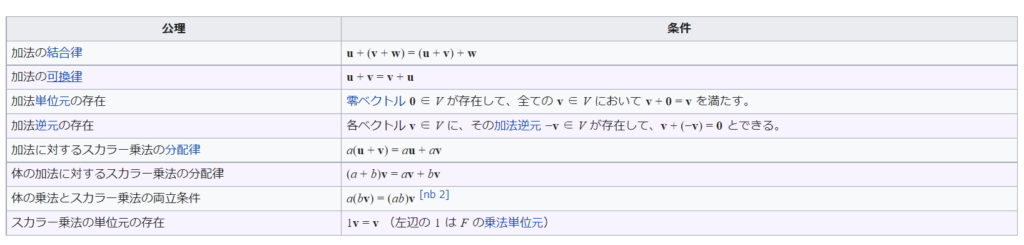
写像のベクトル加法とスカラー乗法の定義でベクトル空間の公理が成り立つのかを確認していきます。
結合法則
ベクトル空間の公理である結合法則が成り立つかを確かめます。
実数だとa + (b + c) = (a + b) + cの等式になります。
写像の場合でも結合法則((f + g) + h) = (f + (g + h)が成立することを証明します。
加法の定義通り変形。
$(f + g) + h:x \to (f(x) + g(x)) + h(x) =f(x) + g(x) + h(x)$
実数の足し算に変形できました。
繰り返しですが、右辺の+は実数の+だからこの操作ができます。
左辺の+は写像の足し算を表しているので、その結果がどうなるのかは定義通り展開してみなければ分かりません。
加法の定義通りに変形
$f + (g + h):x \to (f + (g + h))(x) = f(x) + g(x) + h(x)$
定義通りの変形で結合法則が成り立つことが証明できました。
$((f + g) + h)(x) = (f + (g + h)(x)$
次にスカラー乗法の場合。
同じように定義通り一度実数の形に直して式変形。
$f(gh):x \to f(x)(g(x)h(x)) = f(x)g(x)h(x)$
$(fg)h:x \to (f(x)g(x))h(x) = f(x)g(x)h(x)$
同じ形に変形できました。
交換法則
次に交換法則を確かめます。交換法則はこんな等式。
a + b = b + a,a × b = b × a
まずは加法から。
結合法則と同様に写像f,gで考えます。
$(f + g): \to f(x) + g(x)$
実数同士の足し算は交換法則が成り立ちますので、
$= g(x) + f(x)$
これを再び定義通り変形すると
$= (g + f)(x)$
よって
$(f + g)(x) = (g + f)(x)$
次にスカラー乗法です。
定義通り変形して
$fg:x \to f(x)g(x)$
これも実数同士の乗法になるので、交換法則を適用して定義通り変形
$= g(x)f(x) = (gf)(x)$
よって
$(fg)(x) = (gf)(x)$
0ベクトル
どんな集合の要素xに対しても0しか返さない写像を定義します。
$z:x \to 0$
この写像に写像fを足すと
$f + z:x \to f(x) + z(x) = f(x) + 0 = f(x)$
よって写像の集合の中にも足しても何もしない0写像(ベクトル)が存在していることになります。
ベクトル乗法も同じように定義通り変形。
$fz:x \to f(x)z(x) = f(x)0 = 0$
どんな写像にかけても0になる0写像があります。
同じような論理でスカラー倍しても写像に何もしない1(単位)ベクトルも成立します。
逆ベクトル
ある写像fに対する写像gを定義します。
写像gは常に-f(x)を返します。
$g:x \to -f(x)$
f + gの写像を考えます。
$(f + g):x \to f(x) + g(x) = f(x) + (- f(x)) = 0$
写像の集合にも逆ベクトルと同じ役割を果たす写像があります。
分配法則
分配法則はa(b + c) = ab +acです。
h(f + g) = hf + hgが写像でも成立することを確認します。
既述のスカラー乗法と加法の定義を使って
$h(x)(f + g):x \to h(x)(f(x) + g(x)) = h(x)f(x) + h(x)g(x)$
よって分配法則が成り立ちます。
これで写像がベクトル空間の公理を満たすことを証明できました、多分。
ベクトルの概念を拡張して何がうれしいのかはピンときませんが、ベクトル空間の性質を使って計算処理を簡略化させられるのかなあって直観が働きます。
関数を一般化した写像をベクトル空間として扱えることで$x^{100} +x^{100},x^{99} + 3x^{99}$みたいな多項式がベクトル空間として扱えますからね。便利な定理があるんじゃないですかね、多分。




コメント