 数学とか
数学とか コーシー列と収束する数列
調和数列の面白い性質 僕が面白いと思った性質。 $\sum_{i=1}^{n} \dfrac{1}{n^{1}}⇒∞$ $\sum_{i=1}^{n} \dfrac{1}{n^{2}}⇒\dfrac{π^{2}}{6}$ 指数が1なら発散、...
 数学とか
数学とか  数学とか
数学とか  数学とか
数学とか  数学とか
数学とか  数学とか
数学とか  数学とか
数学とか 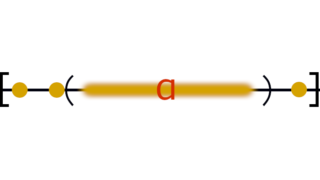 数学とか
数学とか  数学とか
数学とか 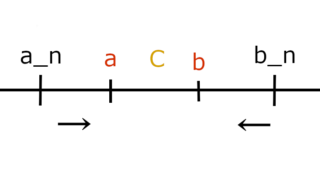 数学とか
数学とか  数学とか
数学とか 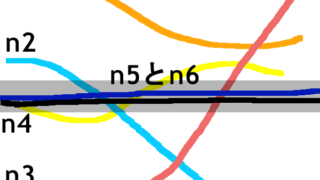 数学とか
数学とか 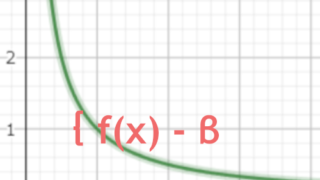 数学とか
数学とか