 暇つぶしに見て
暇つぶしに見て 素人が数学に挑戦 微分で最大値を求める
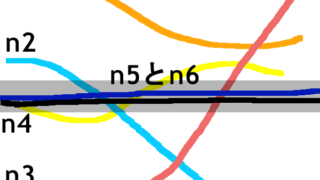
以下の記事で関数列の極限についてはやりました。一応は理解できたんですが、知識は整理されるとその先の細部が散らかっていきますよね。で、疑問が浮かびました。 一様収束ではsup操作を行いますが、この時定義域内の数で$f_n(x)$を最大化するも...
 暇つぶしに見て
暇つぶしに見て 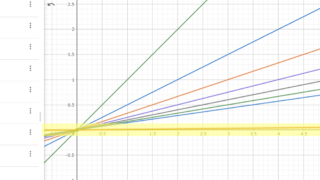 暇つぶしに見て
暇つぶしに見て  選手分析
選手分析 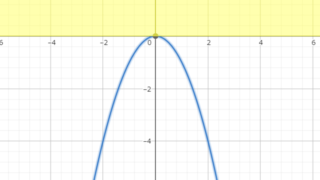 暇つぶしに見て
暇つぶしに見て 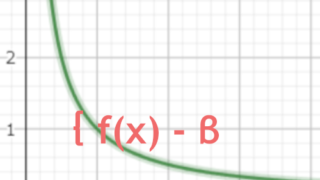 暇つぶしに見て
暇つぶしに見て  トレーニング
トレーニング 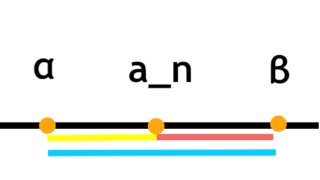 暇つぶしに見て
暇つぶしに見て  技術
技術  暇つぶしに見て
暇つぶしに見て  暇つぶしに見て
暇つぶしに見て  メンタル
メンタル  メンタル
メンタル